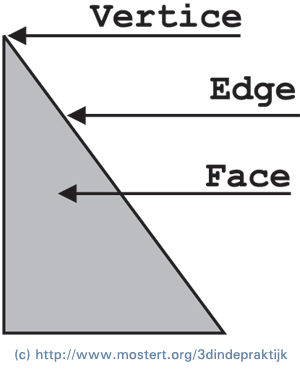
Inleiding tot 3D in de praktijk: Het modelleren van 3D-objecten

Er zijn verschillende methoden om 3D-modellen te modelleren (op te bouwen). Enkele veelgebruikte methoden zijn: polygonen, Spline en NURBS. Veel 3D-programma’s bieden verschillende modelleringsmethoden aan. Ik zal dieper ingaan op polygoon modeling, Spline modeling en NURB-modeling.

Polygoon modeling

Een veelgebruikte manier van 3D-programma’s om objecten te vormen (modelleren) is door gebruik te maken van polygonen. Een polygoon is een gesloten vorm met een oppervlak. De kleinst mogelijke polygoon heeft de vorm van een driehoek. Elk punt van een polygoon waar lijnen samenkomen heet in vaktermen Vertice of Vertex. De randen noemt men Egde en het binnenoppervlak dat wordt omsloten door de lijnen, noemt men Face.

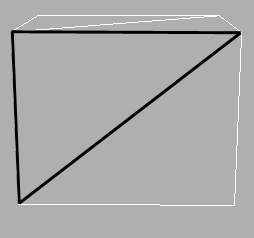
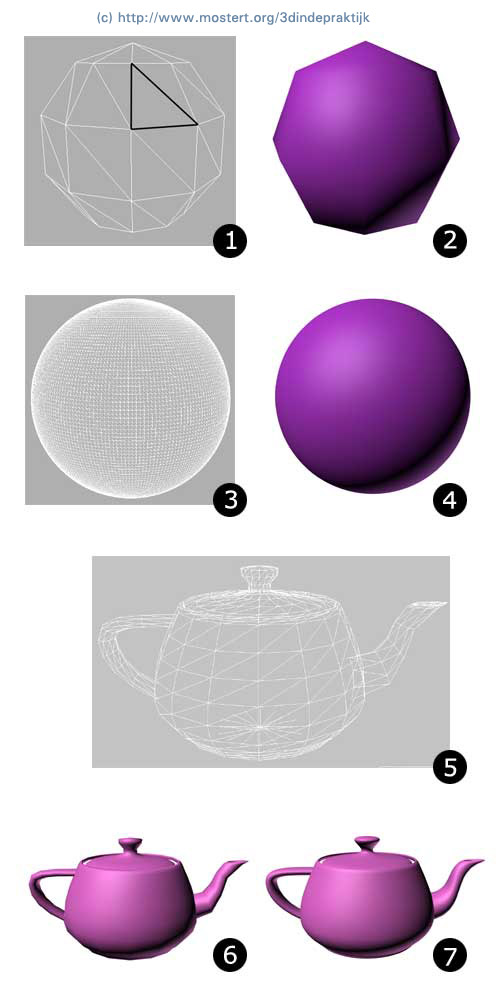
Een object kan dus worden gevormd door de randen van de polygonen aan elkaar te plakken in een bepaalde vorm. Om dit te illustreren ziet u in het volgende figuur een box, waarbij elk vlak van de box wordt gevormd door twee polygonen (als voorbeeld is een van de polygonen zwart gemaakt). De complete box bestaat dus uit 12 polygonen. In de volgende afbeelding ziet u bij 1 een bol die is opgebouwd met behulp van 48 polygonen. De bol oogt vrij grof, maar door het aantal polygonen te verhogen wordt het oppervlak veel gladder. Bij 2 en 3 ziet u hiervan het bewijs doordat dezelfde bol nu is opgebouwd uit 39600 polygonen, wat dus een veel gladdere vorm oplevert. Uiteraard geldt dat bij een toename van het aantal polygonen de computer meer zal moeten rekenen.

Uitleg voorgaande figuren:

1: Een bol opgebouwd uit 48 polygonen.
2: Het oppervlak van de bol met 48 polygonen.
3: Dezelfde bol, maar nu met eengladder oppervlak dankzij de 39600 polygonen.
4: Het oppervlak van de bol met 39600 polygonen.
5: Een theepot opgebouwd uit 1024 polygonen.
6: Dezelfde theepot, maar met 1024 polygonen en een kleurtje.
7: Dezelfde theepot, nu met 262144 polygonen en een kleurtje. Er onstaat een veel gladder en realistischer oppervlak.

De eenvoudigste polygoon heeft de vorm van een driehoek (triangle), maar uiteraard zijn er ook nog andere vormen mogelijk, zoals bijvoorbeeld een vierkant (quad). U zult echter in de meeste gevallen een polygoon in de vorm van een driehoek aantreffen. (Of de polygonen zichtbaar zijn tijdens het maken van het object, is afhankelijk van het 3Dprogramma dat u gebruikt.)

Mesh modeling

Wanneer een 3D-object wordt gevormd door polygonen, dan spreekt men van mesh modeling, of polygonal modeling. Een mesh is een verzameling polygonen die samen een object beschrijft.

De 3D-theepot

De theepot die in veel 3D-programma’s terugkomt is de Utah teapot die rond 1974 door Jim Blinn is ontworpen en vervolgens door Martin Newell en Ed Catmull werd gerenderd. De heren waren op zoek naar een ‘complex’ object om te modelleren. Tijdens het ontbijt kwam de vrouw van Martin Newell met het idee om de theepot hiervoor te gebruiken.

Dit is het eerste object geweest dat niet werd opgebouwd via een set van polygonen. Hierna is de theepot lange tijd als benchmark (snelheidstest) voor renderingsoftware gebruikt. De originele theepot is nog te bezichtigen in het Computermuseum in Boston.

Spline modeling

Bij Spline modeling wordt het oppervlak van een object beschreven aan de hand van gebogen 2D-lijnen (een gebogen lijn noemt men in het Engels een curve) die onderling worden verbonden. Elke curve wordt gedefinieerd aan de hand van een aantal controlepunten die op dezelfde afstand van elkaar staan. Als de computer de controlepunten van alle lijnen kent, dan worden de punten met behulp van een wiskundige formule met elkaar verbonden via een lange gebogen lijn die door alle controlepunten gaat.

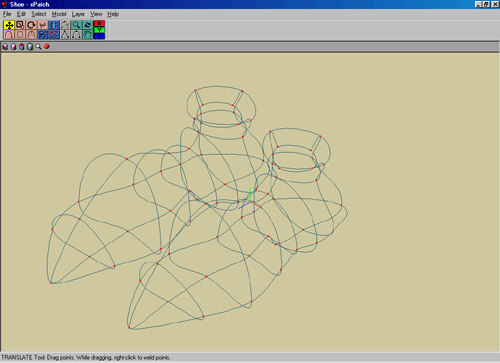
De lijnen worden dus gemaakt aan de hand van wiskundige formules. In de volgende afbeelding ziet u twee schoenen die zijn gemodelleerd met behulp van Splines. De lijnen zijn onderling verbonden en vormen gezamenlijk het oppervlak van de schoenen. In het tweede figuur ziet u het ‘gladde’ resultaat als de schoenen worden geray-traced (zie hoofdstuk 7) met POV-Ray. Een speciaal type Spline is de B-Spline, waarbij de B voor basis staat. Bij de B-Spline worden de eindpunten gedefinieerd en ook de controlepunten, alleen hoeft de lijn niet perse door de controlepunten heen te lopen. Bij Splines is de werking van de controlepunten vergelijkbaar met de zwaartekracht van de aarde. Deze zwaartekracht ‘trekt’ de lijn met behulp van de controlepunten in de juiste richting.

NURB-modeling

De afkorting NURBS staat voor Non-Uniform Rational B-Splines. Simpel samengevat gaat het om een ingewikkelde wiskundige formule die het mogelijk maakt om het oppervlak van (complexe) vormen te beschrijven. Bij NURBS is het mogelijk om de aantrekkingskracht van de controlepunten op de lijnen te regelen. Deze eigenschap duidt men aan met rational. Ook wordt gespecificeerd welk deel van de curve beïnvloed wordt door een bepaald controlepunt. Dit bedoelt men met non-uniform. De vormen die met behulp van NURBS worden gemaakt, zien er vloeiend en afgerond uit.

Pioniers NURBS

P. de Casteljau, werkzaam bij Citroën, en P. Bézier, werkzaam bij Renault, zijn de twee pioniers geweest van het beschrijven van curves en oppervlakten door wiskundige representaties. Hun werk vormde de basis voor de ontwikkeling van NURBS.

Metaballs

Het is ook mogelijk om te modelleren met behulp van Metaballs. In dat geval wordt een object gemaakt uit allerlei ronde vormen. De ronde vormen ‘smelten’ uiteindelijk samen en vormen zo een object.